精密離心機(jī)主要用于線加速度計(jì)等慣性儀表的校準(zhǔn) ［1-2］ 。靜態(tài)半徑是向心加速度的重要組成部分，其 和檢測(cè)   高精度測(cè)量關(guān)系到精密離心機(jī)輸出加速度值的準(zhǔn)確度和 不確定度，進(jìn)而影響加速度計(jì)的校準(zhǔn)和檢測(cè)精度  精 密離心機(jī)靜態(tài)半徑的測(cè)量不確定度**少要比精密離心機(jī)輸出加速度的測(cè)量不確定度高 1 倍甚**更高，對(duì)于加速 度相對(duì)標(biāo)準(zhǔn)不確定度為 10 ^－ 5 或 10 ^－ 6 量級(jí)的精密離心機(jī)， 其對(duì)靜態(tài)半徑測(cè)量方法、測(cè)量系統(tǒng)以及精密離心機(jī)自身   的整體性能都提出了極高要求。目前G內(nèi)外主要有 2 種靜態(tài)半徑測(cè)量方法。一是采用精密量塊和基準(zhǔn)環(huán)或激光自準(zhǔn)直儀等進(jìn)行直接測(cè)
 
［4-6］
量 。該方法受離心機(jī)主軸回轉(zhuǎn)誤差和加速度計(jì)質(zhì)心不確定性影響較大，且測(cè)量環(huán)節(jié)多，測(cè)量精度不高，一般
 
只用于低精度的精密離心機(jī)靜態(tài)半徑測(cè)量。
 
［7］
反算法 測(cè)量靜態(tài)半徑是以重力場(chǎng)下的某個(gè)加速度值( 一般取 1g) 為基準(zhǔn)，調(diào)整精密離心機(jī)轉(zhuǎn)速使待測(cè)加速度計(jì)輸出值等于該基準(zhǔn)值，通過(guò)修正的加速度載荷公式來(lái)反算該狀態(tài)下的工作半徑，以此作為精密離心機(jī)的基準(zhǔn)半徑，其他狀態(tài)的工作半徑等于該基準(zhǔn)半徑加上相應(yīng)的離心機(jī)轉(zhuǎn)盤或大臂的徑向動(dòng)態(tài)變化量。文獻(xiàn)［8］提供的靜態(tài)半徑反算法只考慮向心加速度，適用于一般精度或低精度的精密離心機(jī); 文獻(xiàn)［9］提出的靜態(tài)半徑反算法測(cè)量精度有所提高，但沒(méi)有考慮加速度計(jì)制造及安裝夾具帶來(lái)的俯仰失準(zhǔn)角對(duì)靜態(tài)半徑的影響，而且受加速度計(jì)自身、加速度模型方程以及測(cè)量?jī)x器的系統(tǒng)偏差影響較大，也不能用于高精度精密離心機(jī)的靜態(tài)半徑測(cè)量。此外，采用測(cè)量不確定度來(lái)定量評(píng)價(jià)測(cè)量結(jié)果的精度在G內(nèi)外正成為一種趨
［10-14］，
勢(shì) 然而精密離心機(jī)靜態(tài)半徑測(cè)量不確定度評(píng)定方面的工作G內(nèi)外沒(méi)有公開的文獻(xiàn)報(bào)道，G內(nèi)僅有 2 篇文獻(xiàn)作
［5-6］
了簡(jiǎn)要的敘述和說(shuō)明 。由于高精度精密離心機(jī)及其靜
 
態(tài)半徑測(cè)量很難采用更高精度的儀器或設(shè)備來(lái)檢定、校核其精度，科學(xué)、合理的測(cè)量不確定度評(píng)定模型及評(píng)定方法
 
就變得非常重要。
 
本文提出一種改進(jìn)的反算法，使之能夠應(yīng)用于 10 ^－ 5 以下量級(jí)的高精度精密離心機(jī)靜態(tài)半徑測(cè)量，構(gòu)建測(cè)量系統(tǒng)及不確定度評(píng)定模型，并在自研的 10 ^－ 5 量級(jí)精密離
 
心機(jī)靜態(tài)半徑測(cè)量中得到了較好應(yīng)用。
 
2 靜態(tài)半徑測(cè)量反算法
 
2． 1  測(cè)量原理
 
不同精度等級(jí)的精密離心機(jī)對(duì)靜態(tài)半徑測(cè)量精度要求不同，表 1 給出了不同精度的精密離心機(jī)對(duì)應(yīng)的工作半徑測(cè)量精度要求。工作半徑等于靜態(tài)半徑與動(dòng)態(tài)半徑之和，故靜態(tài)半徑的測(cè)量精度還要高于表 1 中數(shù)值。對(duì)于高精度精密離心機(jī)，靜態(tài)半徑測(cè)量精度要求極高，其測(cè)量過(guò)程中考慮的影響因素增多，這些需要考慮的因素在
 
下文中進(jìn)行分析。
 
［4］
表 1 精密離心機(jī)等級(jí)分類
 
Table 1 Classification of precision centrifuge
 

序號(hào)	精密離心機(jī)	精密離心機(jī)加速度	工作半徑測(cè)量不
	準(zhǔn)確度等級(jí)準(zhǔn)	測(cè)量不確定度	確定度要求
1	0． 1 級(jí)	10 － 3	5 × 10 － 4
2	0． 01 級(jí)	10 － 4	5 × 10 － 5
3	0． 001 級(jí)	10 － 5	7 × 10 － 6
4	0． 000 1 級(jí)	10 － 6	7 × 10 － 7

采用待測(cè)加速度計(jì)輸出值來(lái)反算精密離心機(jī)靜態(tài)半徑的原理如圖 1 所示。靜態(tài)半徑定義為主軸回轉(zhuǎn)軸線到待測(cè)加速度計(jì)有效質(zhì)量中心的距離。待測(cè)加速度計(jì)輸入軸與精密離心機(jī)工作半徑方向重合時(shí)，加速度計(jì)感受到的加速度含有向心加速度，而向心加速度又是靜態(tài)半徑的函數(shù)，故加速度計(jì)輸出值中含有靜態(tài)半徑的信息。結(jié)合加速度計(jì)在重力場(chǎng)下校準(zhǔn)得到的一階靜態(tài)模型方程以及其他測(cè)量分量，按照已確定的精密離心機(jī)輸出到加速度計(jì)輸入軸上的加速度數(shù)學(xué)模型即可反解出此狀態(tài)的靜態(tài)半徑值，精密離心機(jī)在工作狀態(tài)的半徑等于該靜態(tài)半徑值與轉(zhuǎn)盤或大臂的徑向動(dòng)態(tài)變化量之代數(shù)和。
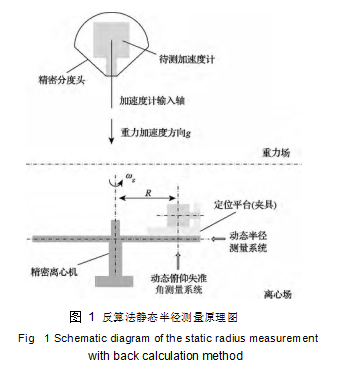
上述反算法測(cè)量靜態(tài)半徑的具體步驟如下:
 
第 1 步: 使用**重力儀測(cè)量當(dāng)?shù)刂亓铀俣戎担⒂镁芊侄阮^等專業(yè)儀表使加速度計(jì)工作軸向與重力加
 
速度方向成不同的角度，讀取加速度計(jì)在 0 ～ 1g 加速度輸入下的電壓或電流輸出值，擬合出加速度計(jì)在重力場(chǎng)下的零次項(xiàng)系數(shù)和標(biāo)度因數(shù)，標(biāo)定出加速度計(jì)的一次靜態(tài)模型方程;
 
第 2 步: 將待測(cè)加速度計(jì)安裝到精密離心機(jī)的定位平臺(tái)或夾具上，調(diào)整加速度計(jì)姿態(tài)使加速度計(jì)輸入軸盡量與精密離心機(jī)工作半徑方向重合。
 
第 3 步: 驅(qū)動(dòng)精密離心機(jī)轉(zhuǎn)動(dòng)，使待測(cè)加速度計(jì)
 
輸出電壓或電流等于 U_g ( U_g 對(duì)應(yīng)的加速度計(jì)輸入值記為 a_g ，通常基準(zhǔn) a_g 約為 1 g 或小于 1 g ) 時(shí)，穩(wěn)定轉(zhuǎn)速，此時(shí)的轉(zhuǎn)速記為 ω_g 。對(duì)于較高精度的精密離心機(jī)，此狀態(tài)下加速度計(jì)輸入軸上感知的加速度除了向

心加速度，還包括重力加速度以及科里奧利加速度
等，根據(jù)加速度載荷簡(jiǎn)化公式，有:
ag  = ω2g Ｒ + λg g ± 2ωg ωε Ｒsin θ				( 1)
為了便于測(cè)量，式( 1) 可以進(jìn)一步轉(zhuǎn)化為:
ag  = ω2g Ｒ + ( λ +  λg ) g ± 2ωg ωε Ｒsin θ				( 2)
式中: Ｒ 為精密離心機(jī)在加速度 ag  下的基準(zhǔn)半徑，即靜
態(tài)半徑; λg  為角速度等于 ωg  時(shí)的俯仰失準(zhǔn)角，rad，包括
動(dòng)態(tài)俯仰失準(zhǔn)角  λg  和靜態(tài)俯仰失準(zhǔn)角 λ; ωε				為地球自
轉(zhuǎn)角速度，rad / s; θ 為精密離心機(jī)所在之地的地球緯度。
對(duì)于北半球G家，精密離心機(jī)逆時(shí)針?lè)较蛐D(zhuǎn)時(shí)式( 1) 、
( 2) 中“± ”號(hào)取“+ ”。
通過(guò)式( 1) 即可反解出靜態(tài)半徑為:
	ag  － λg g		ag  － ( λ +  λg ) g	( 3)
Ｒ =		=
	ω2g  ± 2ωg ωε sin θ		ω2g  ± 2ωg ωε sin θ
式中:
ag  = Ug / k1  － k0				( 4)
式中: k0  為待測(cè)加速度計(jì)的偏值，g 或 m / s2 ; k1  為待測(cè)加
速度計(jì)的標(biāo)度因素，V / g 或 A / g。
聯(lián)合俯仰失準(zhǔn)角和旋轉(zhuǎn)角速度測(cè)量結(jié)果，即可得到
靜態(tài)半徑值。式( 1) 可看出，俯仰失準(zhǔn)角 λg  應(yīng)該包括加
速度計(jì)輸入軸和安裝夾具帶來(lái)的失準(zhǔn)角偏差，然而實(shí)際
采用電子水平儀測(cè)量得到的俯仰失準(zhǔn)角是定位平臺(tái)或離
心機(jī)大臂相對(duì)于地球表面的角度。即使采用其他測(cè)量裝
置也很難直接準(zhǔn)確測(cè)量得到加速度計(jì)輸入軸相對(duì)于地表
的俯仰失準(zhǔn)角。粗略計(jì)算，1″的俯仰失準(zhǔn)角偏差將導(dǎo)致
靜態(tài)半徑 5 × 10 － 6 的相對(duì)誤差，而實(shí)際加速度計(jì)及安裝夾
具的俯仰失準(zhǔn)角不止 1″。因此如何補(bǔ)償不可測(cè)的俯仰失
準(zhǔn)角成為制約上述靜態(tài)半徑測(cè)量方法在高精度精密離心
機(jī)上應(yīng)用的關(guān)鍵。
此外，待測(cè)加速度計(jì)自身分辨率以及各測(cè)量?jī)x器
的誤差將通過(guò)式 ( 3 ) 的間接測(cè)量關(guān)系影響靜態(tài)半徑
反算精度。精密離心機(jī)輸出加速度因素考慮不全面
也會(huì)導(dǎo)致加速度模型式 ( 1 ) 與加速度計(jì)實(shí)際輸入的
值存在偏差，進(jìn)而影響靜態(tài)半徑測(cè)量準(zhǔn)確度。一般精
密離心機(jī)的精度都是高于待標(biāo)定加速度計(jì)的精度 1
或 2 個(gè)量級(jí)，而靜態(tài)半徑測(cè)量精度又必須高于精密離
心機(jī)的精度。表面上看，采用低精度的待測(cè)加速度計(jì)
來(lái)反算高精度的靜態(tài)半徑是矛盾的。實(shí)際上反算法
測(cè)量靜態(tài)半徑只利用了重力場(chǎng)下的加速度計(jì)輸入輸
出特性。重復(fù)性精度方面，待測(cè)加速度計(jì)在重力場(chǎng)下
已校準(zhǔn)得到的一次靜態(tài)模型以及精密離心機(jī)主軸轉(zhuǎn)
速的重復(fù)性精度可以做到很高，能夠滿足靜態(tài)半徑測(cè)
量重復(fù)性精度要求。系統(tǒng)誤差方面，上述反算法受加
速度計(jì)自身和加速度模型方程式 ( 4 ) 以及測(cè)量?jī)x器
的系統(tǒng)偏差影響較大。 2． 2 反算法改進(jìn)               傳統(tǒng)的靜態(tài)半徑反算法是將待測(cè)加速度計(jì)安裝到精   密離心機(jī)上，調(diào)整好加速度計(jì)輸入軸姿態(tài)盡量與精密離 心機(jī)工作半徑方向重合后，直接驅(qū)動(dòng)精密離心機(jī)旋轉(zhuǎn)，記 錄加速度計(jì)輸出值 Ug  和對(duì)應(yīng)的轉(zhuǎn)速 ωg ，其中 Ug  對(duì)應(yīng)的 加速度計(jì)輸入值為 ag ，通常 ag  約為 1g 或小于 1g。本文 提出的靜態(tài)半徑反算法是在調(diào)整好待測(cè)加速度計(jì)輸入軸 盡量與精密離心機(jī)工作半徑方向重合后，進(jìn)行以下 2 次 反算:                         shou先，不啟動(dòng)精密離心機(jī)旋轉(zhuǎn)，直接讀出此時(shí)待測(cè)加 速度計(jì)的輸出電壓或電流值，記為 U0 。由于此狀態(tài)精密 離心機(jī)轉(zhuǎn)速為零，加速度計(jì)輸入軸感知到的加速度只有 俯仰失準(zhǔn)角作用下的重力加速度，即:                           ( 5)   a0  = gλ                               式中: a0  為不啟動(dòng)離心機(jī)時(shí)的待測(cè)加速度計(jì)輸入值; λ 為 加速度計(jì)輸入軸相對(duì)于地表的靜態(tài)俯仰失準(zhǔn)角，rad。 一般電子水平儀測(cè)量得到的是定位平臺(tái)或離心機(jī)大   臂相對(duì)于地表的俯仰失準(zhǔn)角，故將 λ 分為 2 個(gè)角度之和   的形式，即:                                       a0  = g( λ0  + λ1 )           ( 6)                   式中: λ0  為可測(cè)量的定位平臺(tái)或大臂相對(duì)于地表的靜態(tài)   俯仰失準(zhǔn)角，rad。λ1  為不可測(cè)的或測(cè)不準(zhǔn)的加速度計(jì)靜   態(tài)俯仰失準(zhǔn)角，rad。                               其次，啟動(dòng)精密離心機(jī)旋轉(zhuǎn)，使待測(cè)加速度計(jì)輸出電   壓或電流為基準(zhǔn)值 Ug ，穩(wěn)定轉(zhuǎn)速，讀出此時(shí)的精密離心   機(jī)轉(zhuǎn)速 ωg 。有:                               ag  = ω2g Ｒ + ( λ0 + λ1  +   λg ) g ± 2ωg ωε Ｒsin θ ( 7)   式中:  λg  為 ωg  轉(zhuǎn)速下的動(dòng)態(tài)俯仰失準(zhǔn)角，rad。           式( 6) 與( 7) 相減，并利用重力場(chǎng)下已標(biāo)校好的待測(cè)   加速度計(jì)標(biāo)度因數(shù) k1 ，有:                             ag  － a0  － λg g ( Ug  － U0 ) / k1  －  λg g     Ｒ =         ( 8)               =                 2       2                 ± 2ωg ωε sin θ             ωg     ωg  ± 2ωg ωε sin θ     如果調(diào)整待測(cè)加速度計(jì)在精密離心機(jī)定位平臺(tái)上的 姿態(tài)后靜態(tài)俯仰失準(zhǔn)角和方位失準(zhǔn)角仍然較大，其量級(jí) 影響了靜態(tài)半徑的測(cè)量精度，則必須補(bǔ)償二者對(duì)靜態(tài)半 徑的影響，其影響規(guī)律按式( 9) 進(jìn)行補(bǔ)償:     Ｒ =       ( Ug  － U0 ) / k1 －  λg g   ( 9)     (   2 ) cos λ0 cos λ2                               ωg  ± 2ωg ωε sin θ       式中: λ2  為可測(cè)量的方位失準(zhǔn)角，即加速度計(jì)安裝平臺(tái) 在上平面內(nèi)相對(duì)于離心機(jī)半徑方向的偏角，rad。     式( 8 ) 或 ( 9 ) 是本文提出的靜態(tài)半徑計(jì)算模型， 該測(cè)量方法補(bǔ)償了不可測(cè)的加速度計(jì)輸入軸和夾具 安裝俯仰失準(zhǔn)角對(duì)靜態(tài)半徑的影響; 而且通過(guò)兩次加 速度計(jì)的輸入加速度值相減，加速度計(jì)自身、精密離 心機(jī)加速度模型、測(cè)量?jī)x器中的系統(tǒng)誤差以及加速度 計(jì)偏值 k0  被抵消，進(jìn)一步提高了測(cè)量準(zhǔn)確度。此外，與原有反算法相比，該測(cè)量方法不需要對(duì)靜態(tài)俯仰失準(zhǔn)角進(jìn)行測(cè)量，減小了測(cè)量誤差源。改進(jìn)后的靜態(tài)半徑反算法測(cè)量過(guò)程如圖 2 所示。

可編程精密電源采用 Agilent B2900 A 型，為待測(cè)加速度計(jì)提供高精度 ± 15 V 電壓，加速度計(jì)輸出電壓或電流利用 KEITHLE2002 型八位半數(shù)字萬(wàn)用表并經(jīng)
 
GPIB 接口傳輸?shù)?nbsp;PXI 機(jī)箱。角速度測(cè)量系統(tǒng)主要由圓光柵編碼器與頻率計(jì)組成，圓光柵編碼器反饋信號(hào)通過(guò)頻率計(jì)計(jì)算得到精密離心機(jī)的轉(zhuǎn)速，自研的精密離心機(jī)實(shí)際角速度相對(duì)不確定度可控制到 10 ^－ 7 ～
 
10 ^－ 8 量級(jí)。動(dòng)態(tài)俯仰失準(zhǔn)角是通過(guò)電容測(cè)微儀測(cè)量精密離心機(jī)轉(zhuǎn)盤邊沿的上下擺動(dòng)位移量來(lái)間接測(cè)量，利用光柵輸出的 Z 脈沖對(duì)測(cè)點(diǎn)定位，消除轉(zhuǎn)盤表面形狀誤差。由水銀集流環(huán)傳輸?shù)?PXI 機(jī)箱進(jìn)行信號(hào)展寬、濾波等調(diào)理。電容測(cè)微儀為德G米銥公司的 CS 系列，采用定位測(cè)量，其測(cè)量不確定度可以控制到亞微米量級(jí)。
 
4 測(cè)量不確定度評(píng)定模型
 
 
由于誤差評(píng)估固有的缺陷，例如不可量化、誤差定義
 
［15］
與實(shí)際評(píng)定不符 。越來(lái)越多的學(xué)者采用測(cè)量不確定度來(lái)評(píng)價(jià)測(cè)量結(jié)果的精度。高精度精密離心機(jī)對(duì)靜態(tài)半徑測(cè)量精度要求非常高，因此，科學(xué)合理的測(cè)量不確定度
 
評(píng)定變得異常重要。
 
上述改進(jìn)的靜態(tài)半徑測(cè)量模型中，靜態(tài)半徑 Ｒ 通過(guò)間接測(cè)量得到，其測(cè)量誤差源主要來(lái)自于加速度基準(zhǔn) a_g ( 或 U_g ) 、a₀ ( 或 U₀ ) 、動(dòng)態(tài)俯仰失準(zhǔn)角 λ_g 、旋轉(zhuǎn)角速度 ω_g 4 個(gè)分量。測(cè)量模型中的其余常量只要取足夠的有效位數(shù)，引入的不確定度可忽略不計(jì)。需要注意的是 U_g 和 U₀ ( 即 a_g 和 a₀ ) 是同一加速度計(jì)的輸出值，二者明顯相關(guān)。基于測(cè)量不確定度傳遞公
［15］
 
式 ，通過(guò)推導(dǎo)、簡(jiǎn)化，靜態(tài)半徑測(cè)量不確定度傳遞模型為:
 
u_r ( Ｒ) ≈
 

2

( ω ) +

g2

2

(

λ )

2

( a )

a02

2

( a )

2ra0

u' ( a ) u' ( a )

4 u

u

+ u

+

u

－

r

g

a2g

g

r

g

a2g

r

0

ag

r    gr   0

( 10)

 
式中: u_r ( Ｒ) 是靜態(tài)半徑 Ｒ 的相對(duì)標(biāo)準(zhǔn)不確定度; u_r ( ω_g ) 是角速度 ω_g 的相對(duì)標(biāo)準(zhǔn)不確定度; u_r ( a_g ) 是加速度 a_g
的相對(duì)標(biāo)準(zhǔn)不確定度; u( λ_g ) 是動(dòng)態(tài)俯仰失準(zhǔn)角 λ_g  的
 
標(biāo)準(zhǔn)不確定度，rad; u_r ( a₀ ) 是加速度 a₀ 的相對(duì)標(biāo)準(zhǔn)不確定度; u^'_r ( a_g ) 是 a_g 的由系統(tǒng)效應(yīng)引入的相對(duì)標(biāo)準(zhǔn)不確定度; u^'_r ( a₀ ) 是 a₀ 的由系統(tǒng)效應(yīng)引入的相對(duì)標(biāo)準(zhǔn)不確定度; r 是 a₀ 與 a_g 的相關(guān)系數(shù)。
 
一般 a_g ≈g，a_g 和 a₀ 不在同一數(shù)量級(jí)，且 a_g ＞ ＞ a₀ ，其相關(guān)系數(shù)較小可以不考慮，而且 u_r ( a₀ ) 的傳遞系數(shù)很小，則靜態(tài)半徑測(cè)量不確定度傳遞模型可簡(jiǎn)化為:
 
u_r ( Ｒ) ≈  4u²_r ( ω_g )  + u² (  λ_g )  + u²_r ( a_g )     ( 11) 需要說(shuō)明的是，式( 11 ) 的計(jì)算結(jié)果準(zhǔn)確性不比式 ( 10 ) 差，這是由模型本身的特征決定的，為了簡(jiǎn)化評(píng)
 
定復(fù)雜度，本文采用式 ( 11 ) 作為靜態(tài)半徑測(cè)量不確定度的傳遞模型，其不確定度值由加速度值 a_g 、動(dòng)態(tài)俯仰失準(zhǔn)角 λ_g 以及旋轉(zhuǎn)角速度 ω_g 3 個(gè)分量決定。5 10 ^－ 5 量級(jí)精密離心機(jī)靜態(tài)半徑實(shí)測(cè)
 
圖 4 所示是利用所提方法對(duì)研制的加速度相對(duì)標(biāo)準(zhǔn)不確定度為 10 ^－ 5 量級(jí)的精密離心機(jī)靜態(tài)半徑進(jìn)行測(cè)量的實(shí)物圖。安裝就緒后先旋轉(zhuǎn)離心機(jī)到高速借助離心力將螺栓緊固。實(shí)際應(yīng)用時(shí)加速度計(jì)輸入軸指向主軸和相反方向 2 種狀態(tài)的靜態(tài)半徑不相等，可以取兩者的平均作為靜態(tài)半徑值，亦或分開測(cè)量。

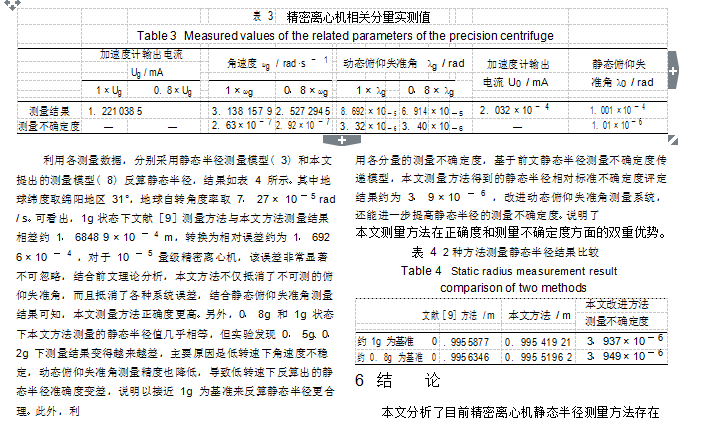
的問(wèn)題，提出一種改進(jìn)的靜態(tài)半徑測(cè)量方法。推導(dǎo)出該測(cè)
 
量方法新的數(shù)學(xué)模型以及對(duì)應(yīng)的測(cè)量不確定度傳遞模型。搭建了測(cè)量系統(tǒng)，對(duì)研制的 10 ^－ 5 量級(jí)精密離心機(jī)靜態(tài)半徑進(jìn)行了實(shí)測(cè)。相同條件下，本文測(cè)量方法與基于文獻(xiàn)［9］的測(cè)量結(jié)果相差 10 ^－ 4 量級(jí)，該偏差對(duì) 10 ^－ 5 和 10 ^－ 6 量級(jí)的精密離心機(jī)影響嚴(yán)重，不可忽視。本文方法的靜態(tài)半徑相對(duì)標(biāo)準(zhǔn)不確定度評(píng)定結(jié)果約為 3． 9 × 10 ^－ 6 。理論分析和實(shí)測(cè)結(jié)果說(shuō)明了本文測(cè)量方法在正確度和不確定度兩方面具
 
有的雙重優(yōu)勢(shì)。
 
反算法測(cè)量的是加速度計(jì)質(zhì)心到主軸回轉(zhuǎn)軸線的距離，準(zhǔn)確度遠(yuǎn)高于基于精密量塊等儀器的直接測(cè)量方法，而且本文提出的反算測(cè)量方法補(bǔ)償了不可測(cè)的俯仰失準(zhǔn)
 
角、加速度模型以及測(cè)量?jī)x器的系統(tǒng)誤差對(duì)靜態(tài)半徑測(cè)量精度的影響，測(cè)量準(zhǔn)確度得到了較大提高。本文提供的測(cè)量方法及不確定度評(píng)定模型可以為 10 ^－ 5 或 10 ^－ 6 量
 
級(jí)的高精度精密離心機(jī)研制提供一定的技術(shù)支撐。